Kipbelasting?

Een week of wat geleden hadden we ons al enigszins in de wereld van het pluimvee begeven door de omschrjving van de nieuwe Liskeshoeve als 'kloek'. Nu heb ik van onze architect een lijvig rapport over de stabiliteit en sterkte van de constructie toegestuurd gekregen, en loop ik tegen de term 'kipbelasting' aan. Nu lijkt het me wel aardig om straks een paar sierkippen rond te hebben stappen, maar niet als onze regering de kip gaat beschouwen als de volgende melkkoe....
Waar hebben we het over? Nadere beschouwing leert dat 'kipbelasting' een gebruikelijke term is in de constructieleer. Het is een instabiliteits-verschijnsel, en komt meestal voor in de combinatie met 'knikken'. Knikken is het buigen van een staaf door een belasting in de lengte- of breedterichting. Kippen is het zijdelings uitbuigen van de staaf loodrecht op de lengte-as samen met het verdraaien om de lengte-as. Het verschil tussen beide belastingen laat zich goed uitleggen met het voorbeeld van een plank over een sloot. Als je de plank plat legt, buigt hij ver door als je erop gaat staan. Als je hem dwars neerlegt, is hij dikker en buigt minder ver door. Maar als je op de smalle kant staat, kipt hij. Hij wijkt uit in horizontale richting en kiept om, roteert. Kippen is dus een buigbelasting.

Als een staaf te ver kipt of knikt, breekt hij, dus bij berekeningen van de constructie moet met deze principes rekening worden gehouden. En omdat ze bij bepaalde belastingen interactie vertonen, is de sterkteberekening verre van eenvoudig.

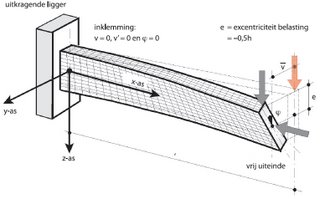Het verschijnsel knik is reeds lang bekend en uitvoerig onderzocht. Al in 1729 stelde Petrus van Musschenbroek dat de sterkte van een staaf belast op druk evenredig is met de inverse van het kwadraat van de lengte. Vijftien jaar later kwam Euler met zijn bekende knikformule die nog steeds als basis dient voor stabiliteitsberekeningen. Kip is een stuk lastiger te beschrijven. Hiervoor dient de eigenwaarde van een stelsel van drie differentiaalvergelijkingen gevonden te worden, en dat vraagt in veel gevallen om uitgebreid rekenwerk met reeksontwikkeling. Tegenwoordig kunnen eindige-elementenpakketten (zoals het door ons adviesbureau gebruikte pakket MatrixFrame) dat monnikenwerk snel uitvoeren.

Uit alle berekeningen blijkt dat de nieuwe Liskeshoeve bestand is tegen alle permanente en veranderlijke belastingen zoals storm en een flink pak sneeuw op het dak. Een hele opluchting!

---